[Algorithm] 펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)
펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)?
펜윅 트리는 세그먼트 트리의 변형으로 세그먼트 트리보다 메모리를 더 절약할 수 있다.
또, 갱신을 O(log n)의 시간에 수행할 수 있으며, 세그먼트 트리보다 구현이 쉽다는 장점이 있다.
구성
펜윅트리는 일반적인 세그먼트 트리와 다르게 기존 배열과 같은 크기로 구성할 수 있다.
펜윅 트리는 다음과 같이 구성한다. 여기서 노란 블럭은 기존 배열, 초록 블럭은 트리 배열이다.

0이 아닌 최하위 비트
펜윅 트리를 초기화하고 업데이트하기 위해선 값을 어떻게 인덱싱하는지 알아야한다.
이때, 0이 아닌 최하위 비트 값을 더해주는 방식을 취한다.
먼저 각 비트의 0이 아닌 최하위 비트를 구하는 방법을 알아보자.
예를 들어 3, 6, 8 값의 최하위 비트를 구한다고 가정해보자
3 = 11(2)
6 = 110(2)
8 = 1000(2)
여기서 각 값의 최하위 비트는 다음과 같다.
3 -> 1(2)
6 -> 10(2)
8 -> 1000(2)
이를 구하기 위해선 다음 연산을 취하면 된다.
int number = 6;
int lsbNotZero = number & -number;이 값을 활용하여 인덱싱을 진행해볼 것이다.
Add 연산
먼저 add 연산의 구현은 다음과 같다. 여기서 n은 트리의 길이를 의미한다.
public void add(int index, int number) {
while(index <= n) {
tree[index] += number;
index += (index & -index);
}
}방금 위에서 설명했던 0이 아닌 최하위 비트를 원래 인덱스에 더해주는 방식을 취했다.
예를 들어, 1부터 진행한다 했을 때 이렇게 하면 다음과 같이 인덱싱이 된다. (빨간 부분이 인덱싱 된 부분이다)

즉 1=1(2) 에서 0이 아닌 최하위 비트를 계속 더해주어, 2=10(2) -> 4=100(2) -> 8=1000(2)로 된 것이다.
이렇게 인덱싱하면서 값을 계속 더해주며 업데이트를 진행해나간다.
Sum 연산
sum 연산의 구현은 다음과 같다.
public long sum(int index) {
long result = 0;
while (index > 0) {
result += tree[index];
index -= (index & -index);
}
return result;
}아까 add연산과는 다르게 0이 아닌 최하위 비트를 계속 빼주며 인덱싱을 진행해 나간다.
예를 들어, 7까지의 합을 구한다 하면 다음과 같이 진행이 된다.
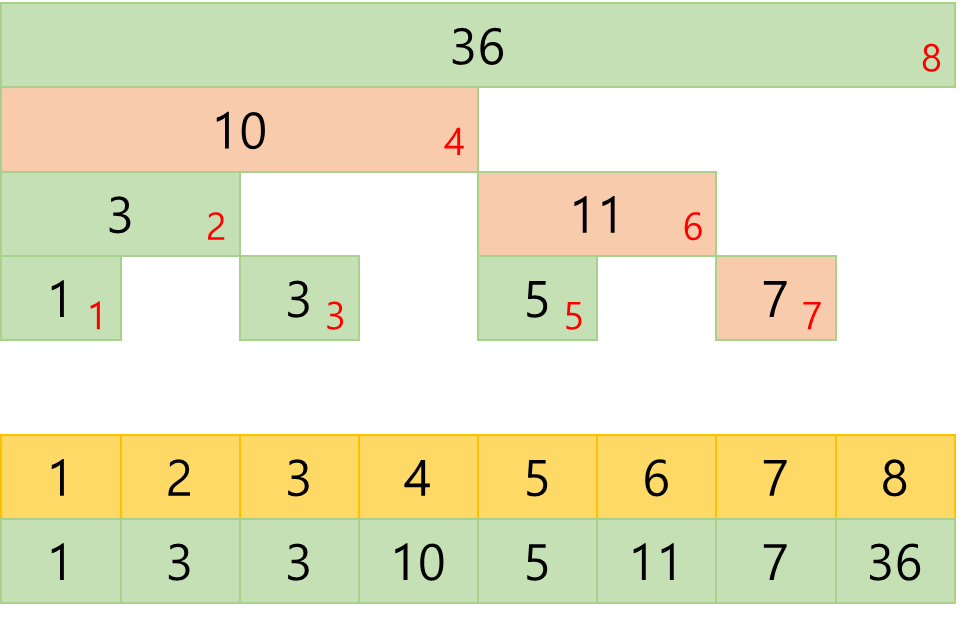
여기선 7=111(2)에서 0이 아닌 최하위 비트를 빼주며, 6=110(2) -> 4=100(2) -> 0 이렇게 진행이된다.
이를 활용하여 특정 구간의 합을 구할 수 있다.
예를 들어, 2에서 5사이의 합을 구하고 싶다면 다음과 같이 구할 수 있다.
sum(5) - sum(1);
구현
코드는 [Baekjoon] 2042: 구간 합 구하기를 기반으로 작성하였다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class FenwickTree {
private static long[] arr;
private static long[] tree;
private static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
String[] input = br.readLine().split(" ");
n = Integer.parseInt(input[0]);
arr = new long[n + 1];
tree = new long[n * 2];
int m = Integer.parseInt(input[1]);
int k = Integer.parseInt(input[2]);
for (int i = 1; i <= n; i++) {
arr[i] = Long.parseLong(br.readLine());
update(i, arr[i]);
}
for (int i = 0; i < m + k; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int command = Integer.parseInt(st.nextToken());
if (command == 1) {
int a1 = Integer.parseInt(st.nextToken());
long b1 = Long.parseLong(st.nextToken());
long diff = b1 - arr[a1];
arr[a1] = b1;
update(a1, diff);
continue;
}
int a2 = Integer.parseInt(st.nextToken());
int b2 = Integer.parseInt(st.nextToken());
sb.append(sum(b2) - sum(a2 - 1)).append("\n");
}
System.out.print(sb);
}
public static void update(int index, long diff) {
while (index <= n) {
tree[index] += diff;
index += (index & -index);
}
}
public static long sum(int index) {
long answer = 0;
while (index > 0) {
answer += tree[index];
index -= (index & -index);
}
return answer;
}
}'Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] 트라이 트리(Trie Tree) (0) | 2023.03.19 |
|---|---|
| [Data Structure] 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2023.02.14 |
| [Data Structure] 세그먼트 트리(Segment Tree) (0) | 2022.09.08 |
| [Data Structure] 이진 탐색 트리(Binary Search Tree) (0) | 2022.08.17 |
| [Data Structure] 우선순위 큐(Priority Queue) & 힙(Heap) (0) | 2022.08.17 |
댓글
이 글 공유하기
다른 글
-
[Data Structure] 트라이 트리(Trie Tree)
[Data Structure] 트라이 트리(Trie Tree)
2023.03.19 -
[Data Structure] 최소 신장 트리(MST, Minimum Spanning Tree)
[Data Structure] 최소 신장 트리(MST, Minimum Spanning Tree)
2023.02.14 -
[Data Structure] 세그먼트 트리(Segment Tree)
[Data Structure] 세그먼트 트리(Segment Tree)
2022.09.08 -
[Data Structure] 이진 탐색 트리(Binary Search Tree)
[Data Structure] 이진 탐색 트리(Binary Search Tree)
2022.08.17