[Algorithm] 페르마의 소정리
글 작성자: SeoArc
페르마의 소정리?
페르마의 소정리는 피에르 드 페르마가 알아낸 정리로서, 정수론의 가장 기본이 되는 정리이다.

이 내용을 간단히 말하면, 임의의 소수 p와 서로소인 수 a에 대해, a^(p-1)을 p로 나눈 나머지는 무조건 1이라는 말이다.
예를 들어, 3^6 = 729를 7로 나누면 나머지는 1이라는 사실을 알 수 있다.
증명
이항정리를 사용한 증명
먼저 페르마의 소정리는 다음과 동치이며, n = 0일 경우는 자명하다.
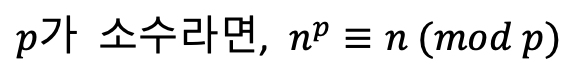
이항정리에 의하면

여기서, 0 < n < p이면
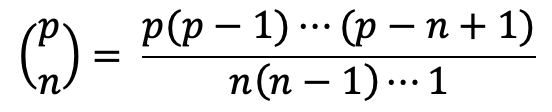
은 p의 배수이다. 따라서,

는 항상 성립하는 명제이다.
같은 방법으로
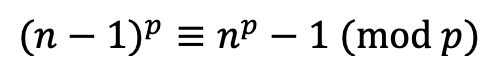
도 항상 성립한다. 따라서 n일 때 성립한다 가정하면, n+1, n-1일 때도 성립한다. 즉, 모든 정수 n에 대해 이 공식이 성립한다는 것을 알 수 있다.
기약잉여계를 사용한 증명
기약잉여계?

먼저 a와 p가 서로소라고 하자. 이때 1a, 2a, ..., (p-1)a는 mod p에 대해 서로 합동이 아니다. 또한 이 중에서 p의 배수인 것은 없으므로, 이 ka들을 p로 나눈 나머지들의 집합은 {1, 2, ..., p-1}와 같다. 이때 전부 곱한 것을 생각하면 다음이 성립한다.

여기서 (p-1)!은 p와 서로소이므로 양변에서 나누어줄 수 있다. 따라서
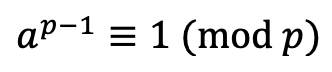
활용
이 정리를 이용해 다음과 같은 식을 도출 할 수 있다.

'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] 보이어-무어 알고리즘(Boyer-Moore Algorithm) (0) | 2023.04.04 |
|---|---|
| [Algorithm] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2023.03.30 |
| [Algorithm] 플로이드-워셜(Floyd-Warshall) (0) | 2023.03.12 |
| [Algorithm] 상계/하계(Upper Bound/Lower Bound) (1) | 2023.03.11 |
| [Algorithm] 이진 탐색(Binary Search) (0) | 2023.03.11 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 보이어-무어 알고리즘(Boyer-Moore Algorithm)
[Algorithm] 보이어-무어 알고리즘(Boyer-Moore Algorithm)
2023.04.04 -
[Algorithm] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
[Algorithm] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
2023.03.30 -
[Algorithm] 플로이드-워셜(Floyd-Warshall)
[Algorithm] 플로이드-워셜(Floyd-Warshall)
2023.03.12 -
[Algorithm] 상계/하계(Upper Bound/Lower Bound)
[Algorithm] 상계/하계(Upper Bound/Lower Bound)
2023.03.11