[Algorithm] 크루스칼 알고리즘 (Kruskal Algorithm)
글 작성자: SeoArc
크루스칼 알고리즘 (Kruskal Algorithm)?
크루스칼 알고리즘은 그래프 내의 모든 간선의 가중치를 확인하고 가장 작은 가중치부터 확인해서 최소 신장 트리를 만드는 알고리즘으로, 탐욕적인(greedy) 방법을 통해 구현할 수 있다.
greedy?
- 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것
- 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다.
- 크루스칼 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
구현
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다.
- 해당 간선을 현재의 MST의 집합에 추가한다.
동작 과정
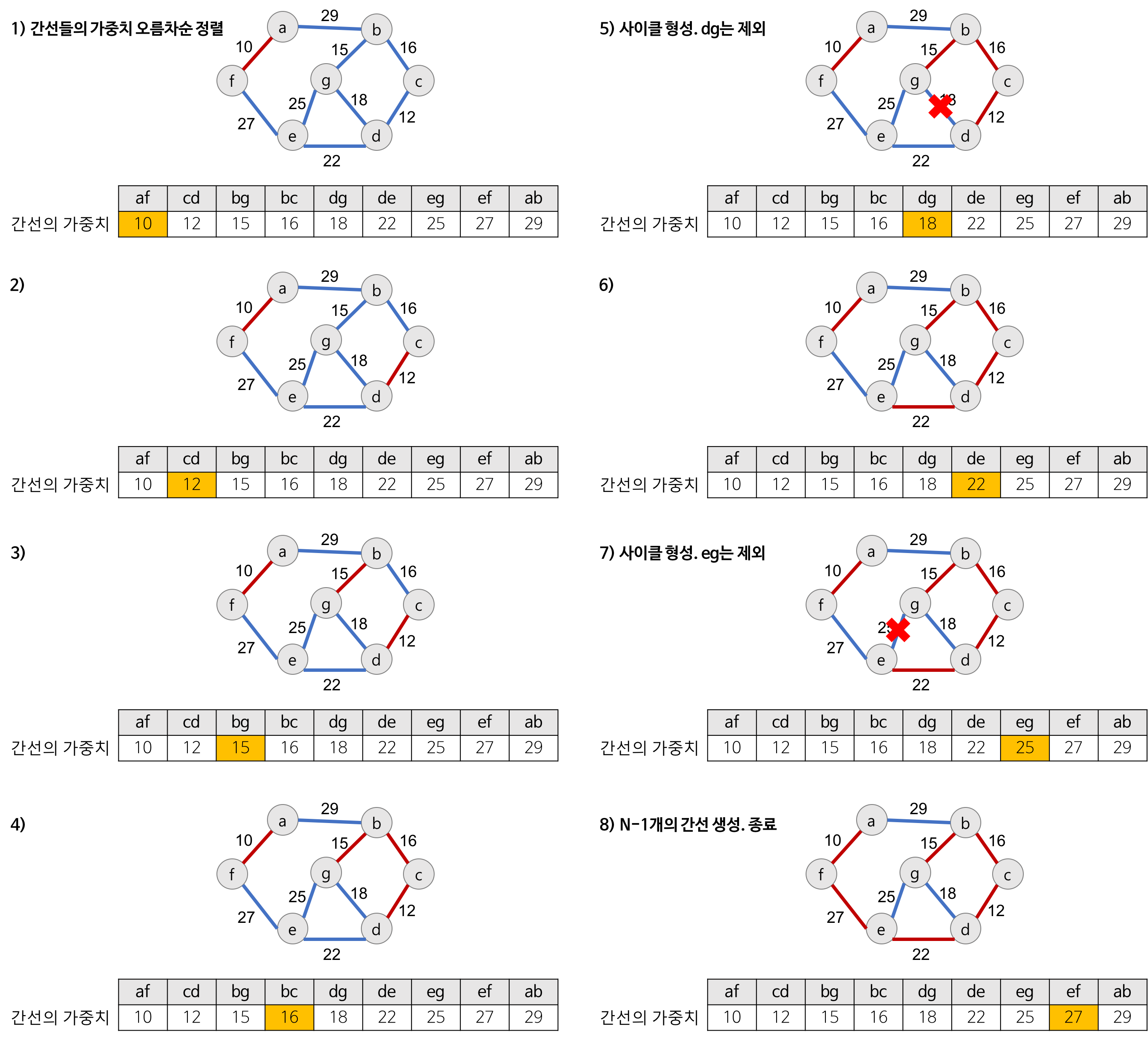
코드
크루스칼 알고리즘을 구현하기 위해선 먼저 유니온-파인드 알고리즘의 이해가 필요하다.
자세한 내용은 다음 링크를 참고하자
[Algorithm] 유니온-파인드(Union-Find)
[Algorithm] 유니온-파인드(Union-Find)
유니온-파인드(Union-Find)? Union-Find는 여러 개의 노드가 존재할 때, 어떤 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다. 방법 같은 그래프에 속하는지 어떻게 판별할까? 다음 그림을
seoarc.tistory.com
다음 코드는 baekjoon: 1197 - 최소 스패닝 트리를 기준으로 작성하였다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
class Edge {
private final int vertex1;
private final int vertex2;
private final int weight;
public Edge(int vertex1, int vertex2, int weight) {
this.vertex1 = vertex1;
this.vertex2 = vertex2;
this.weight = weight;
}
public int getVertex1() {
return vertex1;
}
public int getVertex2() {
return vertex2;
}
public int getWeight() {
return weight;
}
}
public class Kruskal {
private static List<Edge> edges;
private static int[] parent;
private static int res;
private static boolean check;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
edges = new ArrayList<>();
parent = new int[10001];
String[] ve = br.readLine().split(" ");
int v = Integer.parseInt(ve[0]); // 정점의 개수
int e = Integer.parseInt(ve[1]); // 간선의 개수
// 자기 자신을 루트로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
for (int i = 0; i < e; i++) {
String[] input = br.readLine().split(" ");
int vertex1 = Integer.parseInt(input[0]);
int vertex2 = Integer.parseInt(input[1]);
int weight = Integer.parseInt(input[2]);
edges.add(new Edge(vertex1, vertex2, weight));
}
// 가중치를 기준으로 오름차순 정렬
edges.sort(Comparator.comparingInt(Edge::getWeight));
for (int i = 0; i < e; i++) {
// 정점1과 정점2를 union -> 다른 언어의 경우 예약어 주의
union(edges.get(i).getVertex1(), edges.get(i).getVertex2());
if (check) {
res += edges.get(i).getWeight();
}
}
System.out.println(res);
}
public static int getParent(int x) {
// 자기 자신이면 루트 노드이므로 return
if (x == parent[x]) {
return x;
}
// 부모 노드를 재귀로 호출하며 탐색
return parent[x] = getParent(parent[x]);
}
public static void union(int a, int b) {
check = false;
a = getParent(a);
b = getParent(b);
// 이미 같은 그래프에 속했으면 return -> 사이클이 있다는 의미
if (a == b) {
return;
}
// 같은 그래프가 아니라면 a를 부모 노드로 설정
parent[a] = b;
check = true;
}
}'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] 프림 알고리즘(Prim's algorithm) (0) | 2023.02.28 |
|---|---|
| [Algorithm] 다익스트라(Dijkstra) (0) | 2023.02.26 |
| [Algorithm] 유니온-파인드(Union-Find) (0) | 2023.02.19 |
| [Algorithm] 백트래킹(BackTracking) (0) | 2023.02.14 |
| [Algorithm] 비트마스킹(bitmasking) (0) | 2023.02.10 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 프림 알고리즘(Prim's algorithm)
[Algorithm] 프림 알고리즘(Prim's algorithm)
2023.02.28 -
[Algorithm] 다익스트라(Dijkstra)
[Algorithm] 다익스트라(Dijkstra)
2023.02.26 -
[Algorithm] 유니온-파인드(Union-Find)
[Algorithm] 유니온-파인드(Union-Find)
2023.02.19 -
[Algorithm] 백트래킹(BackTracking)
[Algorithm] 백트래킹(BackTracking)
2023.02.14